IQM Academy - Foundations of Quantum Computing

Bringing it all together

The first two qubit gate we just learned about is called CNOT (Controlled NOT) gate. It applies a X gate to the target qubit (in the image below, the second qubit) if and only if the control qubit (in the image below, the first one) is in state \(\ket{1}\). If the control qubit is in state \(\ket{0}\) it does nothing.

But what happens if the control qubit is not in state \(\ket{0}\) or state \(\ket{1}\) but in a superposition state?

Combining CNOT and Hadamard

Apply a Hadamard gate H to the first qubit before applying the CNOT gate to bring it into uniform superposition. Then perform some measurements again with different input values

My measurements

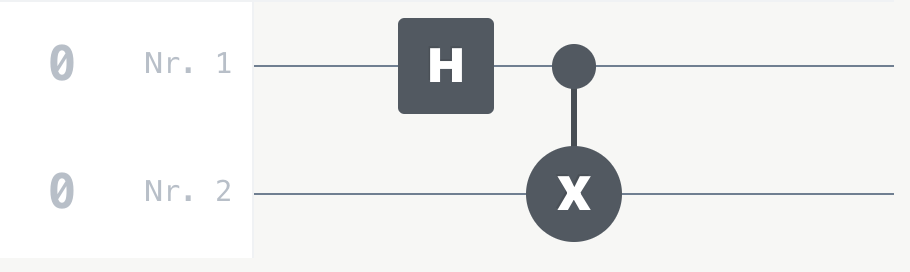
Starting with \(\ket{0}\) as the initial state for both qubits. If we measured the first qubit to be \(\ket{1}\). What is correct about measuring the second qubit?

A

It will be measured either \(\ket{0}\) or \(\ket{1}\) randomly.
B

It will be measured \(\ket{1}\).
C

It will be measured \(\ket{0}\).

That's right! If the control qubit is in a superposition, the measurement result of the target qubit depends on which value the control qubit will ultimately be measured as. The states of the two qubits are thus entangled. If one measures the state of one of the qubits, the state of the other qubit is automatically known.

Not quite. If the control qubit is in a superposition, the measurement result of the target qubit of the target qubit depends as which value the control qubit will ultimately be measured as. The states of the two qubits are thus entangled. If one measures the state of one of the qubits, the state of the other qubit is automatically known.