IQM Academy - Foundations of Quantum Computing

Entangled – A bond for life

As you have experienced with your measurements, the result of a circuit in quantum computers is often not fixed from the beginning. No matter how many qubits we have, when we make a measurement, we get a particular result only with a given probability. In order to get a reliable result about the state and to be able to distinguish between the different superposition states, we again have to perform a large number of measurements to determine this probability accurately.

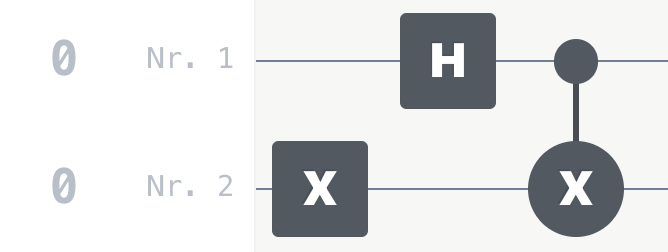
This becomes exciting in connection with the CNOT gate: If the control qubit is in a superposition, the measurement result of the target qubit depends on which value the control qubit now takes. With this, we have learned another special feature of qubits:

Two qubits can be entangled with each other. An entangled state can not be expressed with one state for each qubit. However, if we then measure the state of one of the qubits, you automatically know the state of the other qubit.

Entanglement allows us to create states that we would not have achieved in any other way – for example, a state where we measure \(\ket{00}\) 50% of the time and \(\ket{11}\) 50% of the time.

Use all available gates to create a state with a 50% probability of getting \(\ket{10}\) as output and a 50% probability of getting \(\ket{01}\) as output.

Hint

You can create a CNOT gate by arranging an X gate and a gate in the same column, selecting both, and clicking C in the toolbar.

The animation shows you how to create a CNOT gate.

My measurements

After 1000 measurements we get the following distribution:

Is the state with 50% probability of getting \(\ket{10}\) as output and a 50% probability of getting \(\ket{01}\) as output also an entangled state?

A

Yes.
B

No

That's right! When measuring one qubit as 0, we already know the other qubit will be measured 1.

Not quite. Actually, when measuring one of the qubits 0, we already know the other qubit will be measured 1.

The 2022 Nobel prize in physics was awarded to Alain Aspect, John F. Clauser, and Anton Zeilinger for their work on entanglement. The experimental tools they developed helped to make quantum computation and other quantum technologies a reality.