The rotated planar code

There is another surface code called the rotated planar code[Bombin, 2007]. As its name suggests, this code is obtained by rotating the planar code of distance $d$ counter-clock-wise by 45°. Then, one identifies a square lattice with $d$ data-qubits on each side. This square lattice (along with some additional stabilizers) are kept, and the rest of the qubits are discarded. The following image shows how the rotated planar code is obtained:

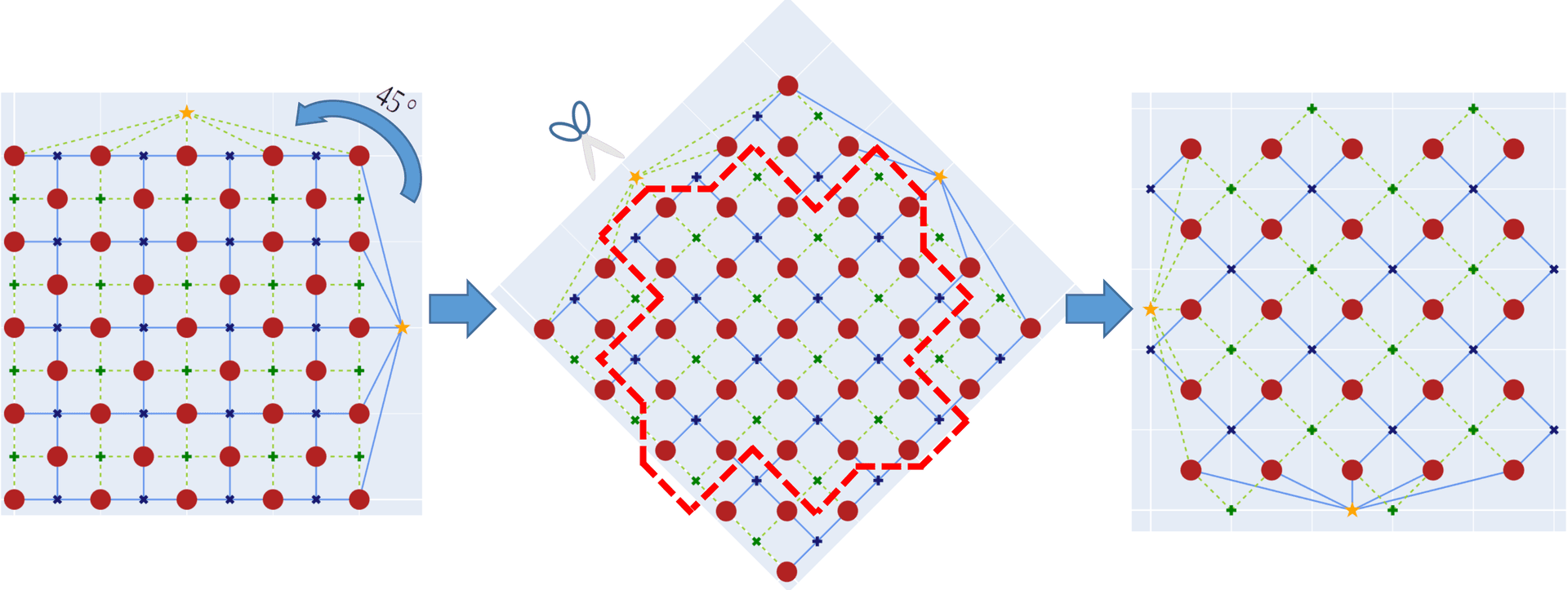
The rotated planar code has become of great interest because it poses the same advantages as the planar code: it contains only nearest-neighbor interactions and it can be easily scaled. However, it also presents an additional advantage over the planar code: a rotated planar code of distance $d$ can be constructed using nearly half the number of qubits needed for a planar code with equivalent distance. This further leads to a reduced number of stabilizers, implying fewer required measurements.

The rotated planar code has $d^2$ data qubits and $d^2-1$stabilizers, where $d$ is the distance of the code. This means that this code only has one degree of freedom, or said differently, it encodes one logical qubit.

In the rotated planar code, above the top side and below the bottom side, we can find additional $Z$-type stabilizers. Outside of the left and right sides, we find $X$-type stabilizers. The logical $\bar{X}$ is defined by the application of $X$ gates on the bottom side of the lattice, and the $\bar{Z}$ is obtained by applying $Z$ gates on the left side of the lattice.